Expected shortfall
Expected shortfall (ES) is a risk measure, a concept used in finance (and more specifically in the field of financial risk measurement) to evaluate the market risk or credit risk of a portfolio. It is an alternative to value at risk that is more sensitive to the shape of the loss distribution in the tail of the distribution. The "expected shortfall at q% level" is the expected return on the portfolio in the worst  % of the cases.
% of the cases.
Expected shortfall is also called conditional value at risk (CVaR), average value at risk (AVaR), and expected tail loss (ETL).
ES evaluates the value (or risk) of an investment in a conservative way, focusing on the less profitable outcomes. For high values of  it ignores the most profitable but unlikely possibilities, for small values of
it ignores the most profitable but unlikely possibilities, for small values of  it focuses on the worst losses. On the other hand, unlike the discounted maximum loss even for lower values of
it focuses on the worst losses. On the other hand, unlike the discounted maximum loss even for lower values of  expected shortfall does not consider only the single most catastrophic outcome. A value of
expected shortfall does not consider only the single most catastrophic outcome. A value of  often used in practice is 5%.
often used in practice is 5%.
Expected shortfall is a coherent, and moreover a spectral, measure of financial portfolio risk. It requires a quantile-level  , and is defined to be the expected loss of portfolio value given that a loss is occurring at or below the
, and is defined to be the expected loss of portfolio value given that a loss is occurring at or below the  -quantile.
-quantile.
Contents |
Formal definition
If 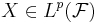 is the payoff of a portfolio at some future time and
is the payoff of a portfolio at some future time and 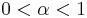 then we define the expected shortfall as
then we define the expected shortfall as 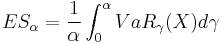 where
where 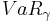 is the Value at risk. This can be equivalently written as
is the Value at risk. This can be equivalently written as ![ES_{\alpha} = -\frac{1}{\alpha}\left(E[X 1_{\{X \leq x_{\alpha}\}}] %2B x_{\alpha}(\alpha - P[X \leq x_{\alpha}])\right)](/2012-wikipedia_en_all_nopic_01_2012/I/70827891456d538676c1da2ecc16007e.png) where
where 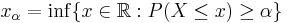 is the lower
is the lower  -quantile. The dual representation is
-quantile. The dual representation is
where 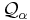 is the set of probability measures which are absolutely continuous to the physical measure
is the set of probability measures which are absolutely continuous to the physical measure  such that
such that 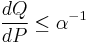 almost surely.[1] Note that
almost surely.[1] Note that 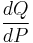 is the Radon–Nikodym derivative of
is the Radon–Nikodym derivative of  with respect to
with respect to  .
.
If the underlying distribution for  is a continuous distribution then the expected shortfall is equivalent to the tail conditional expectation defined by
is a continuous distribution then the expected shortfall is equivalent to the tail conditional expectation defined by ![TCE_{\alpha}(X) = E[-X|X \leq -VaR_{\alpha}(X)]](/2012-wikipedia_en_all_nopic_01_2012/I/f8a19f526cf116193e22a7f892e2c5ab.png) .[2]
.[2]
Informally, and non rigorously, this equation amounts to saying "in case of losses so severe that they occur only alpha percent of the time, what is our average loss".
Examples
Example 1. If we believe our average loss on the worst 5% of the possible outcomes for our portfolio is EUR 1000, then we could say our expected shortfall is EUR 1000 for the 5% tail.
Example 2. Consider a portfolio that will have the following possible values at the end of the period:
Notice that, for convenience, the outcomes have been ordered from worst (first row) to best (last row). Also, the probabilities add up to 100% by construction.
| probability | ending value |
|---|---|
| of event | of the portfolio |
| 10% | 0 |
| 30% | 80 |
| 40% | 100 |
| 20% | 150 |
Now assume that we paid 100 at the beginning of the period for this portfolio. Then the profit in each case is (ending value-initial investment) or:
| probability | |
|---|---|
| of event | profit |
| 10% | −100 |
| 30% | −20 |
| 40% | 0 |
| 20% | 50 |
From this table let us calculate the expected shortfall 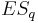 for a few (arbitrarily chosen) values of
for a few (arbitrarily chosen) values of  :
:
 |
expected shortfall 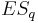 |
|---|---|
| 5% | −100 |
| 10% | −100 |
| 20% | −60 |
| 40% | −40 |
| 100% | −6 |
To see how these values were calculated, consider the calculation of 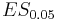 , the expectation in the worst 5 out of 100 cases. These cases belong to (are a subset of) row 1 in the profit table, which have a profit of -100 (total loss of the 100 invested). The expected profit for these cases is -100.
, the expectation in the worst 5 out of 100 cases. These cases belong to (are a subset of) row 1 in the profit table, which have a profit of -100 (total loss of the 100 invested). The expected profit for these cases is -100.
Now consider the calculation of 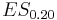 , the expectation in the worst 20 out of 100 cases. These cases are as follows: 10 cases from row one, and 10 cases from row two (note that 10+10 equals the desired 20 cases). For row 1 there is a profit of -100, while for row 2 a profit of -20. Using the expected value formula we get
, the expectation in the worst 20 out of 100 cases. These cases are as follows: 10 cases from row one, and 10 cases from row two (note that 10+10 equals the desired 20 cases). For row 1 there is a profit of -100, while for row 2 a profit of -20. Using the expected value formula we get
Similarly for any value of  . We select as many rows starting from the top as are necessary to give a cumulative probability of
. We select as many rows starting from the top as are necessary to give a cumulative probability of  and then calculate an expectation over those cases. In general the last row selected may not be fully used (for example in calculating
and then calculate an expectation over those cases. In general the last row selected may not be fully used (for example in calculating 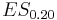 we used only 10 of the 30 cases per 100 provided by row 2).
we used only 10 of the 30 cases per 100 provided by row 2).
As a final example, calculate 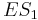 . This is the expectation over all cases, or
. This is the expectation over all cases, or
Properties
The expected shortfall 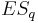 increases as
increases as  increases.
increases.
The 100%-quantile expected shortfall 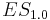 equals the Expected value of the portfolio. (Note that this is a special case; expected shortfall and expected value are not equal in general).
equals the Expected value of the portfolio. (Note that this is a special case; expected shortfall and expected value are not equal in general).
For a given portfolio the expected shortfall 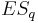 is worse than (or equal) to the Value at Risk
is worse than (or equal) to the Value at Risk 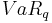 at the same
at the same  level.
level.
Dynamic expected shortfall
The conditional version of the expected shortfall at the time t is defined by
- Failed to parse (PNG conversion failed;
check for correct installation of latex, dvips, gs, and convert): ES_{\alpha}^t = \operatorname*{ess\sup}_{Q \in \mathcal{Q}_{\alpha}^t} E^Q[-X|\mathcal{F}_t]
This is not a time-consistent risk measure. The time-consistent version is given by
- Failed to parse (PNG conversion failed;
check for correct installation of latex, dvips, gs, and convert): \rho_{\alpha}^t = \operatorname*{ess\sup}_{Q \in \tilde{\mathcal{Q}}_{\alpha}^t} E^Q[-X|\mathcal{F}_t]
such that
See also
Methods of statistical estimation of VaR and ES can be found in Embrechts et al. [6] and Novak [7].
References
- Rockafellar, Uryasev: Optimization of conditional Value-at-Risk, 2000.
- Acerbi, Tasche: Expected Shortfall, a natural coherent alternative to Value-at-Risk, 2001
- Rockafellar, Uryasev: Conditional Value-at-Risk for general loss distributions, 2002.
- Acerbi: Spectral measures of risk, 2005
- ^ Föllmer, H.; Schied, A. (2008) (pdf). Convex and coherent risk measures. http://wws.mathematik.hu-berlin.de/~foellmer/papers/CCRM.pdf. Retrieved October 4, 2011.
- ^ "Average Value at Risk" (pdf). https://statistik.ets.kit.edu/download/doc_secure1/7_StochModels.pdf. Retrieved February 2, 2011.
- ^ Detlefsen, Kai; Scandolo, Giacomo (2005). "Conditional and dynamic convex risk measures" (pdf). Finance Stoch. 9 (4): 539–561. http://www.dmd.unifi.it/scandolo/pdf/Scandolo-Detlefsen-05.pdf. Retrieved October 11, 2011.
- ^ Acciaio, Beatrice; Penner, Irina (2011) (pdf). Dynamic convex risk measures. http://wws.mathematik.hu-berlin.de/~penner/Acciaio_Penner.pdf. Retrieved October 11, 2011.
- ^ Cheridito, Patrick; Kupper, Michael (2010). Composition of Time-Consistent Dynamic Monetary Risk Measures in Discrete Time.
- ^ Embrechts P., Kluppelberg C. and Mikosch T., Modelling Extremal Events for Insurance and Finance. Springer (1997).
- ^ Novak S.Y., Extreme value methods with applications to finance. Chapman & Hall/CRC Press (2011). ISBN 9781439835746.
![ES_{\alpha} = \inf_{Q \in \mathcal{Q}_{\alpha}} E^Q[X]](/2012-wikipedia_en_all_nopic_01_2012/I/11dc6d9bac32a5940d5537c73cb2f008.png)
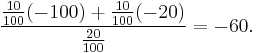
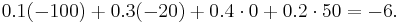
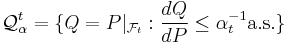 .
.![\tilde{\mathcal{Q}}_{\alpha}^t = \left\{Q << P: \mathbb{E}\left[\frac{dQ}{dP}|\mathcal{F}_{\tau%2B1}\right] \leq \alpha_t^{-1} \mathbb{E}\left[\frac{dQ}{dP}|\mathcal{F}_{\tau}\right] \; \forall \tau >= t \; \mathrm{a.s.}\right\}.](/2012-wikipedia_en_all_nopic_01_2012/I/556556f7f9bd7bf1c91a1dba49a84d95.png)